Imaginary music (PRELIMINARY ENGLISH VERSION)
[home] <<summary <preceding
next>
[Français
![]() ]
]
The musical color contains all that who cannot describe by the classic music theory, who draws lines without worrying about the color or about the thickness of the line; henceforth the counterpoint, the harmony and the rhythm seem incomplete or unsuitable to represent the contents of the works within the reach of techniques and of the human potential of creation.
There is the classic notion of tone, which is related to the musical instrument emitting the sound. We recognize effectively a sound object thanks to the tone and to the pitch, or pitches for a chord. It is a subtle and accurate notion at the stage of the listening, because the ear can perceive very tiny differences of tone, but the words fail to reliably transmit this perception by speaking or writing, because these words are limited by the known list of sounds of the reference instruments.
Fortunately the acoustic science can here provide its contribution. It brings the basic concepts which answer this need of objective description. Let us return to the raw phenomenon: a sound object reaches the ear thanks to a wave of pressure which makes vibrate the eardrum. The shape of this vibration is what we call "acoustic signal". When we describe the properties of the acoustic signal, we then describe the properties of the sound color.
We promize to not bore our reader with the mathematics. There is just a small effort to ask him: understand the representation of Fourier. This physicist explained at the beginning of the nineteenth century that any signal can result from the superimposing of a series of periodic (vibratory) signals. Thus, instead of representing the complex shape of the signal of pressure which reaches the eardrum, it is simpler to represent the series (or spectre) of frequencies which compose it:
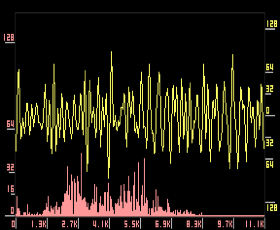
Figure 1 :
Two manners to represent a signal:
At the top: the shape of the signal, below: the spectre of the signal
According to the theorem of Fourier, any shape of signal can be obtained by the superimposing of pure sinusoidal signals. To reconstitute the exact sound of the sound object; it is thus enough to know the list of these signals, with for each :
its amplitude,
its frequency,
its time lag (phase).
The diagram which draws the distribution of the acoustic energy (amplitude) according to every component frequency is called spectre of frequencies .
This diagram is completed by the spectre of phases, which associates a time lag with every component frequency. The mathematical operation which makes calculate the shape of spectres from the shape of the acoustic signal is called transformation of Fourier.
Conversely, if we stack again the sine curves of the spectre of frequencies by respecting the time lags of the spectre of phase, we synthetize again the original acoustic signal (it is the inverse Fourier transformation).
When the signal is periodic (vibratory), we say that it is a sound, the pitch of which corresponds to the fundamental frequency ( the lowest). Other frequencies being multiple of the fundamental are called harmonics. The spectre of a sound is thus a suite of regularly spaced out sticks, the sizes of which correspond to the importance of every harmonic in the constitution of the tone. The vertical bars display as at the right of the spectre as the sound is high-pitched. The vertical bars are as numerous as the sound is rich in harmonics.
|
|
|
|
|
|
Figure 2 : spectres of sounds and noises
When the signal is non-periodic (aperiodic), its pitch is indistinct: we say that it is a noise, and its spectre is a continuum of nearby frequencies, grouped or not around some basic frequencies.
All the noises are not alike: they have a different spectre because they have a different color. And as the colourers who consider that the white is the sum of all the colors, the acousticians also speak about white noise, which contains all the frequencies with the same amplitude. Thus the spectre of the white noise is perfectly horizontal.
The imagination did not go as far as defining notions of blue, red or green noise. Nevertheless we consider as pink noise (or Gaussian noise) a spectre in the shape of bell (curve of Gauss) centred on a frequency.
The analysis of Fourier provides a completely impartial definition of the fact what is a noise against a sound. However, in the common life, people often express quite other opinion: for anybody, any unpleasant or unwanted sound emission in circumstances is considered as noise (it can be the noise of the traffic, or the neighbour pianist who does not stop practising scales).
The word "noise" is connoted by the desirable or not nature of the signal. Even the technician calls noise all the signals, periodic or not, which perturb or mask the signal which interests him. It can be about the white noise (as the squelch of an amplifier), or a low sound due to 50Hz magnetic fields.
A common error consists in believing that the analysis of Fourier provides the key of the sound colors and the rational method to describe all the instrumental tones, and so that should be enough to establish the collection of the frequency spectres of all the sound objects that we wish to describe, in particular musical instruments.
In music, the perfectly harmonic sound does not exist: it always includes a part of noise: it is either the striking of the hammer of piano, the squeaking of the bow, the plucking of string, or the consonants in the singing. This observation joins the mathematical theory, which imposes that a perfectly harmonic sound is of infinite duration (it always existed and will always exist), and naturally it is never the case here on earth.
So we can explain why the first electronic synthesizers, on base of oscillators, very interesting to generate new sounds, imitate with pale colors the traditional instruments. To reproduce exactly the transitions (attack, release, diverse variations: vibrato,...), which are essential noises for the sound color, is impossible for the not digital electronics. And it is this dynamics which contains the major part of the recognizable characteristics of the sound objects.
Exactly, the ear recognizes sound objects in the same way as it recognizes the phonemes of the language :
the dynamics of the signal articulates consonants,
the harmonic composition emits the vowels.
To illustrate this speach, the diagrams which follow represent the frequencial analysis of some vowels and consonants (brackets correspond to International Phonetic Alphabet symbols).
|
The sound [ i: ] (english "ee") The sound [ i ] correspond to an almost perfect sinusoid ; the light deformations of the waveform are natural to the tone of the here recorded voice. The trace of the frequency spectre (below to the left) shows that this waveform occupies a narrow range. |
|
|
The sound [ u: ] (english 'blue") The sound [ u: ] is richer : the waveform contains a variation which is due to a double frequency harmonic which clearly appears in the frequency spectre |
|
|
The sound [ a: ] (english "arm") The vowel [ a: ] waveform is much more complex. The frequency spectre comes to our help to show the spreading of the harmonics. Effectively this vowel is felt as "warmer" than the others. |
|
|
The sound [ f ] The consonant [ f ], which results from the breath of the air which blows between teeth and lips, illustrates well enough the notion of white noise. The waveform is perfectly random, and the spectre widely spread out. |
|
|
The sound [ Here the air passes in the tube formed by the " mouth in mixing bowl". The noise of breath is centred around a frequency according to the shape of the mouth. The sound [ |
|
|
The sound [ r ] Caused by fast occlusions, this sound [ r ] (there are many pronunciations of [ r ] in the various languages) is an example of noise occupying a limited range of the frequency space. |
|
We analized every sound object as consisted of a sound and a noise. Now let us see which effects are produced when we play with them.
The human ear, in the best conditions, can hear only the vibrations of frequencies allowed by his own audiogram, which is an individual version of isophones curves of Fletcher, included between 20 Hz and 20 000 Hz (20 kHz).
Thus any frequency outside is perfectly inaudible: to make slide a sound beyond these limits has the same effect for the listener as to remove it.
Furthermore, for a given individual, the right ear and the left ear have a different perception, and make even a different analysis of sound colors. Indeed, ears are respectively connected to the left and right cervical hemispheres, which, we know it, participate in different ways in the cognitive process.
If we mix two audible frequencies f1 and f2, we can hear a resulting mix which contains, besides f1 and f2:
an higher frequency f3 = f1 + f2 (if it is audible);
a lower frequency f4 = f1 - f2 (if it is audible)).
If f1 and f2 are very close, the (inaudible) low frequency manifests itself by a beating of the energy of the sound, which increases and decreases alternately as a tremolo. When both frequencies are almost equal, the beating is so slow that it generates significant moments of extinctions of the sound.
If on the contrary we cause the beating of a unique sound by a slow tremolo frequency, according to the law of addition of frequencies, we add to the basic signal two other signals shifted above and down by the tremolo frequency.
We thus have a symmetry of the effects:
two close sounds (almost in accord) generate a beating;
a sound modulated by a tremolo beating generates two close sounds.
For the ear, the distinction is not possible a priori, and it needs the other criteria to determine if one or two sound objects are in question, by integrating the part of noise constitutive of the tone, or the spatial separation.
To modulate a frequency consists in making vary its value around its basic frequency.
If the frequency of modulation is a rather slow oscillation so that the listener perceives it clearly, it shifts in a alternative way all the frequencies of the signal together (vibrato, siren).
If the modulation frequency is a too fast vibration, it changes the spectre by making it sweep the nearby frequencies, and thus transforms the sound into noise.
When we modulate an audible frequency by another audible frequency, we generate a big quantity of harmonics of both frequencies, the color of which depends on the amplitude of the modulator signal. This process is exploited in electronic sound synthesis (John Chowning's invention, followed by the production of the Yamaha DX 7 synthesizer and by its derived instruments).
This operation consists in multiplying all the frequencies of the spectre of a signal by the same value, what does not change the shape of the spectre, but shifts it towards the high or low pitches.
Practically, we can notice this effect when we change the speed of reading of a tape recorder, or when the sound source moves enough fast so that there is Doppler effect, which makes sounds to slide towards the high when the source gets closer and towards the low when it goes away. The Doppler effect is also the cause of the " Leslie " effect of Hammond organs.
The transposition, for the harmonics sounds, is also a simultaneous multiplication of all the used frequencies.
The practice of the scratch of vinyl records by the DJ exploits the frequency shiftings realized by changing the speed of rotation of the turn-table.
The filtering consists in modifying the shape of the spectre, and thus the sound color, by weakening or by strengthening some frequencies. A filter does not introduce new frequencies into the spectre of a signal. We know the classic electronic filters: low-pass (or high-cut, or HF), high-pass (or low-cut, or LF), band-pass, band-cut, frequency-cut (notch).
The propagation of sounds in the air also produces an effect of filtering, by weakening more the higher frequencies than the lower frequencies.
The ground passes on mainly the lower frequencies, and thus the more a sound source is located near the ground, the more the lower frequencies are strengthened with regard to the higher. In conclusion, the distance causes a filtering by relative weakening of the higher frequencies.
Some architectural or natural forms, by facilitating or by discriminating the propagation of some wavebands, are also filters (cf. noise-reducing walls by the sides of motorways, a forest, a theater hall with or without the crowd).
NB : we do not speak here about the effects of filtering by convolution functions performed through digital processors, which, formally, can transform any signal into any other wished signal.
When an object, or an electronic circuit, resounds accordingly to one or several particular frequencies of a sound signal, it concentrates all the sound energy which it re-emits on these only frequencies of resonance.
This phenomenon thus adds a fixed frequency pure sound, which can be interpreted by the ear either as an integrated part of the original sound object, or, more rarely, as the new sound object "woken" by the first one.
Examples : glazing, frame of piano, stretched out guying, resonators of vibraphone or marimba.
The previously seen limits of the listening do not authorize every sound object to occupy all the room, in the same way as a stage does not free each of the dancers to use all the surface without precaution towards the others.
Thus, sound objects have to share this space together, and this causes interactions and relations.

Figure 3 : interactions between objects in the color dimension
In practice, if a frequency is used at the same time by two or several objects, it cannot be any more discerned as belonging to the one or to the other one. As a consequence, only the frequencies particular to the color of each object allow the distinction between objects.
If two objects have the same fundamental, they are said in accord; but they can damage mutually themselves by the beating, and destroy themselves when their signals are in opposition of phase. Technically it can be interesting then to delete the fundamental of one of the both; the experts of the sound mixing know well this problem of " jam " in the low frequencies. We can also find this problem at the level of shared harmonics.
Concerning the noises, the problem is much more serious.
Indeed, sounds occupy the ground of the frequencies only by punctually standing "sticks" , what leaves a big latitude for the coexistence. On the other hand, a noise occupies an as wider area as its color is rich, what implies a difficult coexistence.
In illustration, let us take the example of a conversation between two persons, at first "live", then through the telephone. The direct sound allows to use all the audible frequencies (between 20 and 20 000 Hz), while the telephone "bandwidth" is limited by the frequencies 300 and 3 000 Hz, what damages the conditions of coexistence.
If both persons speak at the same time, with a little of attention, the listener located in the same room can understand at least the speech of one speaker; it is a little more difficult from a nearby room, but it is very difficult at the telephone.
If both persons sing simultaneously, we understand without any trouble the one or the other singing, even at the telephone, especially if there is one male and one female voice, from which tessituras are distant of one octave.
From an acoustic point of view, the spoken language contains a bigger part of noise than the sung language. The sung language contains more harmonics sounds.
The range of the frequencies audible by the human ear thus possesses a relatively limited room for the coexistence of several sound objects. To remedy it and in particular facilitate the polyphony, civilizations imposed fixed heights scales.
In a natural and universal way, we mark out the heights of sounds by octaves, that is by multiplying every time the frequency by two.
To widen the possibilities of harmony (pleasantly associate heights from different instruments and from voices), the European music divided the octave into twelve degrees, at first, historically, by a series which allows perfectly on-key chords (by superimposing the harmonics in coincidence to master the beatings), then, to allow the transposition by fixed heights instruments (keyboards), by cheating a little over the accuracy thanks to the " temperament" .
A good idea of the physical realization of the European scale of degrees is provided by the logarithmic disposal of frets along the neck of a guitar.
Other cultures produced different scales, or make music without agreeing of a scale because a scale is not necessary for the monodic music.
.
Imaginary music ISBN 978-2-9530118-0-7 copyright Charles-Edouard Platel
[home] <<summary <preceding top^ next>